Info 24/mar/2015: "Enigma matemático que durava mais de 60 anos é finalmente solucionado"
Ciências e Tecnologia 25/mar/2015: "Enigma de Fermi-Pasta-Ulam resolvido após 60 anos"
Phys.org 23/mar/2015: "Mathematicians solve 60-year-old problem"
Press release da Unviersidade de East Anglia s.d. "UEA mathematician solves 60-year-old problem"
Press release do Instituto Politécnico Rensselaer (RPI) 23/mar/2015: "A mathematical explanation for the Fermi-Pasta-Ulam system problem first proposed in 1953"
Artigo no PNAS 23/mar/2015: "Route to thermalization in the α-Fermi-Pasta-Ulam system"
Só a Info e o comunicado à imprensa do RPI mencionam a contribuição de Mary Tsingou na formulação original do problema.
Usando a base de dados do Google Acadêmico, a busca por "Fermi-Pasta-Ulam problem" e "Fermi-Pasta-Ulam-Tsingou problem" tem os resultados representados no gráfico abaixo (Fig.1).
Figura 1. Menções ao problema como de "Fermi-Pasta-Ulam" (FPU) ou de "Fermi-Pasta-Ulam-Tsingou" (FPUT) em artigos científicos por período. Fonte: Google Scholar.
Em 2008, o físico francês Thierry Dauxois da Escola Normal Superior em Lyon publicou um artigo que resgata a participação essencial de Mary Tsingou (depois, Mary Tsingou Menzel) na questão.
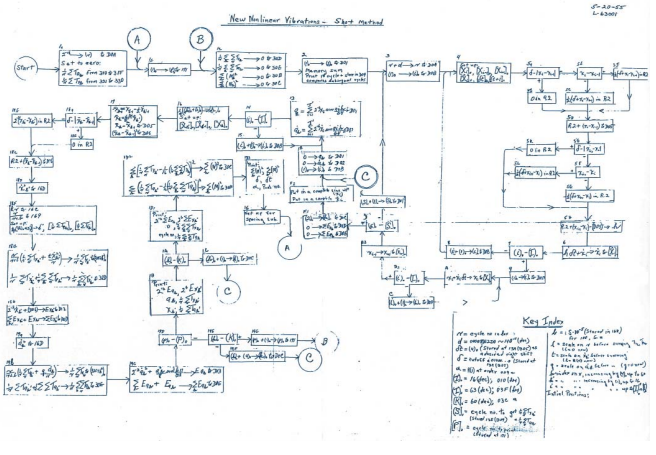
Embora o relatório original de 1955 leve a assinatura apenas de Enrico Fermi, físico italiano; John Pasta, físico computacional americano; Stanislaw Ulam, matemático americano de origem polonesa (então parte do Império Austro-Húngaro); Mary Tsingou fez boa parte do trabalho de elaboração do algoritmo e programação (Fig. 2) - uma tarefa nada trivial, nem um pouco fácil com os poucos recursos computacionais (mesmo em laboratório como Los Alamos, com seus famosos monstrengos adequadamente denominados "Mathematical Analyzer, Numerator, Integrator, and Computer", MANIAC para os íntimos) disponíveis.
Figura 2. Algoritmo desenvolvido por Mary Tsingou para abordagem computacional do problema de Fermi-Pasta-Ulam-Tsingou. Fonte: Dauxois 2008.
Dauxois faz um breve relato da vida de Tsingou. Nascida em Milwaukee, no estado americano de Wisconsin, em 1928, cresceria na América da Grande Depressão, mudando-se com a família para a Bulgária em 1936 atrás de melhores condições de vida. Mas em junho 1940, seguindo recomendação da embaixada americana, retornaram para os EUA devido ao aumento da tensão no subcontinente balcânico (a Segunda Guerra Mundial já corria solta na Europa Central; em outubro, a Grécia viria a ser invadida pela Itália).
Ela formou-se em 1951. No ano seguinte, buscou uma vaga em Los Alamos, contando com o apoio de uma professora sua de equações diferenciais avançadas. Mesmo a matemática sendo um campo ainda fechado às mulheres, a Guerra da Coreia provocava uma redução de mão de obra masculina, então, ela, juntamente com outros recém-graduados, foram contratados para fazerem cálculos matemáticos à mão.
Foi das primeiras pessoas a conseguirem programar o recém-construído MANIAC I. O principal uso do trambolho era, claro, relacionado ao desenvolvimento de armas, mas ocasionalmente encontravam brechas para utilizar o brinquedo para algo mais produtivo: resolução de problemas da Física e jogo de xadrez. Tsingou e Pasta foram os primeiros a desenvolverem gráficos no MANIAC.
Fermi, professor em Chicago, visitava Los Alamos apenas brevemente. Mas foi dele a ideia de utilizar o computador não apenas para realizar cálculos padrões, e, sim, também para testar hipóteses físicas. Nascia disso a experimentação numérica e a era das simulações computacionais científicas.
Com sua experiência na programação do computador, proximidade com Pasta e Ulam, foi incumbida a ela a tarefa de desenvolver os algoritmos da simulação de um cristal unidimensional - sem saber o resultado surpreendente que iriam obter.
Modelando os átomos como massas conectadas linearmente por molas que obedeciam à lei de Hooke, mas com um pequeno termo não-linear, observaram que, ao contrário do previsto, a energia não acabava sendo partilhada igualmente pelo sistema, mas o sistema, de tempos em tempos, voltava à sua condição original. A busca pela resolução desse paradoxo levou ao desenvolvimento do campo dos sólitons (ondas localizadas com propriedades de partículas) e o problema FPUT se tornou central também nos estudos sobre o caos.
Em 1955, Tsingou obteria seu mestrado. Em 1958, casou-se com com Joseph Menzel, que conheceu no próprio Los Alamos. Além do problema FPUT, ela também trabalhou com soluções numéricas para a equação de Schrödinger e trabalhou com von Neumann na modelagem de mistura de fluidos com densidades diferentes. Além de contribuir com estudos sobre o programa Guerra nas Estrelas da administração Reagan.
Aposentou-se em 1991 e desde então mora com o marido nos arredores de Los Alamos.
Por que, tendo papel tão essencial, Mary Tsingou foi deixada de lado? Poderia ser por, apesar de ter botado a mão na massa, não haver participado da elaboração do artigo. Mas ela participou da produção dos gráficos e Fermi, morto um ano antes, não tinha como colaborar com o manuscrito, porém foi listado como primeiro autor.
Não era a primeira vez que o efeito Matilda aprontava das suas, não seria a última. Talvez o caso mais famoso de uma mulher alijada do reconhecimento seja de Rosalind Franklin e sua contribuição para o desvendamento da estrutura do ADN - creditada, normalmente apenas a Watson e Crick, e, ocasionalmente a Wilkins também.
Em sua linha final, Dauxois propõe: "Let us refere from now on to the Fermi-Pasta-Ulam-Tsingou problem". ["Chamemos de agora em diante de problema Fermi-Pasta-Ulam-Tsingou"]. Alguns atenderam à convocação, mas são somente 15 trabalhos publicados desde então (e indexados na base do Google Acadêmico) referem-se a FPUT contra mais de 400 que citam apenas FPU.